- 源由
在機率計算及統計分析中,各種分佈的機率密度函數(Probability Density Function, PDF)、累積分佈函數(Cumulative Distribution Function CDF) 及分位數(Quantile) 等函數值常常用到。傳統上,有兩種方法取得這三個函數值:一種是由定義去計算,另一種則是查表。計算太耗費時間,查表則需有表帶在身邊。加上初學者對這些函數值的意義並不是很清楚,因此這兩種方法對他們而言並不容易,可能使他們失去學習興趣。以下這個Applet 可幫助學習者快速又方便的查出他們所要的函數值,並且藉由圖形釐清這三個函數值的意義。
- 方法
此 Applet 用到的方法包括常用的九個連續分佈及六個離散分佈的機率密度函數、累積分佈函數以及分位數三個函數值(Rice, 1995)。 - 特性及應用
利用繪圖的方式把各分佈的機率密度函數、累積分佈函數以及分位數的具體意義呈現出來,釐清這三個函數的基本概念。教授者可以利用此Applet 作為輔助工具,幫助學習者瞭解關於機率密度函數、累積分佈函數以及分位數三個函數值所代表的含意,並減少計算的負擔及查表的不便。 - 範例
我們以連續的常態分佈 (normal distribution) 及離散的二項分佈 (binomial distribution) 為例來做說明。首先,以常態分佈的PDF、CDF 及Quantile 為例。假設我們想找N(0, 1) 在 x=2 的PDF、CDF 及p=0.5 的Quantile:在「選擇欲求之種類」中點選PDF、「選擇分佈」的選項中點選Normal Distribution,然後在所出現的空格中分別填上x=2、mu=0、sigma2=1,按確定鈕後,我們就可以在下方的欄位得到所要計算的PDF 近似0.054 ,並可在右邊看到它在圖形中所代表的意義。此時若要計算CDF只要在「選擇欲求之種類」中點選CDF選項,然後直接按確定即可,由所計算出之結果知其CDF 近似0.977。若是要計算Quantile,除了要把「選擇欲求之種類」改成Quantile 外,還要把p 的值改為0.5,由所得之結果可知此時之Quantile 為 0。
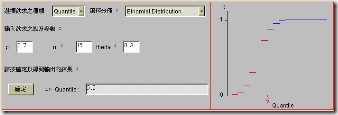
其次以二項分佈的PDF、CDF 及Quantile 為例。假設我們想要找B(15, 0.3) 在x=5 的PDF、CDF 及p=0.7 的Quantile:在「選擇欲求之種類」中點選PDF、「選擇分佈」的選項中點選Binomial Distribution,然後在所出現的空格中分別填上x=5、n=15、theta=0.3,按確定鈕後,我們就可以在下方的欄位得到所要計算的PDF 近似0.206,並可在右邊看到它在圖形中所代表的意義。若要計算CDF,只要在「選擇欲求之種類」中點選CDF 選項,直接按確定即可,由所計算出之結果知其CDF 近似0.7216。如果要計算Quantile,除了要把「選擇欲求之種類」改成Quantile外,還要把p 的值改為0.7,由所的之結果可知此時之Quantile 為5。
由下面的圖可以知道, PDF (圖一或圖四) 指的是所給定的點它所會發生的機率值函數, CDF (圖二或圖五) 是指將所給定的點之前的所有機率值累加所得到的機率值函數,而Quantile (圖三或圖六) 則為CDF 的反函數。並且可以發現CDF 是一個遞增到1的離散階梯函數或遞增到1的連續函數。
(圖一) 常態分佈PDF
(圖二) 常態分佈CDF
(圖三) 常態分佈Quantile
(圖四) 二項分佈PDF
(圖五) 二項分佈CDF
(圖六) 二項分佈Quantile
- 操作
使用這個 Java Applet 時,必須先選擇所要求的函數種類,例如 PDF (機率密度函數)、CDF (累積分佈函數) 或 Quantile (分位數) ,再選擇欲計算之分佈,例如:常態分佈、均勻分佈、幾何分佈等。選完函數的種類及分佈之後,給定所選分佈的參數及所想要計算的數值。按確定按鈕,就可以得到所要的函數值,並看到這些函數值在整個幾何圖形中所代表的意義。






沒有留言:
張貼留言